¡Hola!
Hoy vamos a reducir dos problemas de geometría a uno.
Basta con reflexionar antes de lanzarse a aplicar "la receta" de cada problema. La clave es plantear la posibilidad de resolver ambos con la misma solución general, aplicando nuevas restricciones compatibles y equivalentes.
Problema 1. Hallar las circunferencias tangentes a las rectas r y s, y pasa por el punto P.
Problema 2. Hallar las circunferencias tangentes a la recta s, y pasa por los puntos P y Q (P') .
Se parte del problema 1 y para resolverlo se va a reducir al problema 2. Una de las rectas se obviará en un momento dado y se buscará un punto nuevo que de primeras no es un dato del problema 1, pero sería equivalente a uno de los dos puntos que aparecen en el problema 2.
Y para ello se va a utilizar la herramienta Geogebra y el teorema de la altura y el teorema del cateto además del concepto de potencia de un punto respecto de una circunferencia:
"Los conceptos de potencia de un punto respecto de una circunferencia permiten abordar los problemas con un enfoque unificador, de forma que cualquier enunciado de tangencias o incidencias en general se puede reducir a uno más genérico que denominaremos Problema Fundamental de Tangencias."
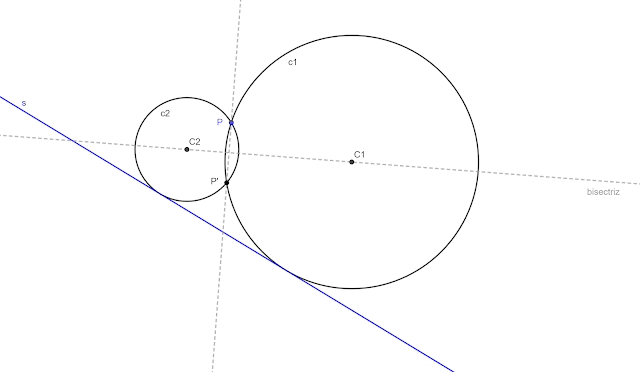
Lo primero de todo. Recordad que los centros de las circunferencias tangentes (c1 y c2) a dos rectas (r y s) pasan por la bisectriz del ángulo formado por las rectas. Así que la solución (son dos) será la siguiente:
Como se pretende reducir el problema 1 al problema 2, se necesita encontrar otro punto por el que pasarán las circunferencias solución. Este otro punto común a ambas circunferencias, P', es el simétrico de P respecto de la bisectriz que se ha hallado en el paso anterior. ¿Por qué? Las circunferencias son simétricas respecto de la línea que une sus centros, por lo que todos sus puntos son simétricos respecto de ésta. Una de las rectas (r) ya no hace falta por lo que se oculta para simplificar.
A continuación, para no despistar, se ocultarán las dos circunferencias solución. Para continuar: de acuerdo al concepto de potencia, el valor de la potencia del punto A (intersección de la recta PP' y s) respecto de cualquier circunferencia que pase por P y P' será el mismo, por lo que se traza una circunferencia auxiliar cualquiera que pase por ambos puntos.
Para obtener el valor de la potencia es necesario hallar el segmento de tangencia desde A respecto de la circunferencia auxiliar (W1 y W2). ¿Cómo? Para ello se trazará el arco capaz de 90º desde A respecto de la Circunferencia auxiliar, los puntos de corte de éste con la circunferencia auxiliar son los puntos de tangencia, o puntos dobles de contacto.
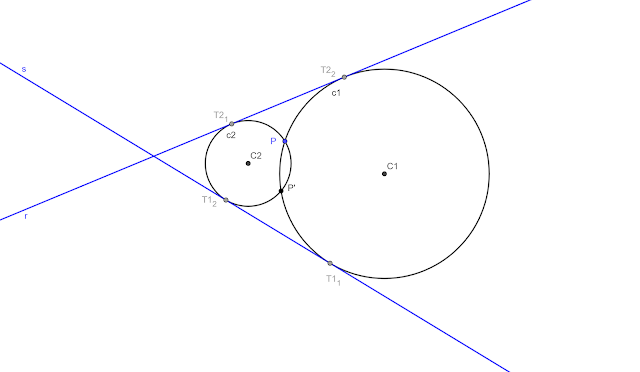
Como se ha hallado la circunferencia cuyo radio es la potencia de las circunferencias respecto del punto A, su intersección con la recta s serán los puntos de Tangencia con ésta de las circunferencias solución.
Una vez tenemos la recta donde se encuentran los centros de las circunferencias (bisectriz), y dos puntos de cada una de ellas (P, T11 y T12) podemos trazar las circunferencias. Recordad que el centro de las circunferencias se encuentra en la mediatriz entre dos puntos de ésta.
Y ahora sí, si volvemos a mostrar la recta r, comprobamos que las dos circunferencias que se han trazado son tangentes a ella. Por lo que el problema 1 se puede reducir al problema 2.
¡Nos vemos en el siguiente manjar!
:)







Comentarios
Publicar un comentario